The first GTACS of the year will be at IDC Herzliya, Tue, Oct 29th, 2019 at the Efi Arazi School of Computer Science.
The event will be held in the Erazi/Ofer building. The seminar talks will be in Lecture Room C.109, and coffee breaks in the M.Sc. lab (there will be signs once you reach the building).
PROGRAM
09:30-10:15 Coffee & Registration
10:15-11:00 Niv Gilboa, Fully Linear PCPs and their Cryptographic Applications
11:00-11:30 Coffee break
11:30-12:15 Gilad Asharov, OptORAMa: Optimal Oblivious RAM
12:15-13:45 Lunch
13:45-14:30 Hayim Shaul, How to Trade Efficiency and Accuracy using Fault-Tolerant Computation
14:30-14:45 Coffee break
14:45-15:35 Iftach Haitner, A Tight Parallel-Repetition Theorem for Random-Terminating Interactive Arguments
15:30-15:45 Coffee break
15:45-16:30 Noga Ron-Zewi, Local Proofs Approaching the Witness Length
ABSTRACTS
Fully Linear PCPs and their Cryptographic Applications
Niv Gilboa, Ben Gurion University
Abstract:
In the first part of this talk, we will introduce a new type of proof system, called fully linear probabilistically checkable proofs ("fully linear PCPs"). Fully linear PCPs apply naturally to the setting in which the verifier has only an encryption of the statement being proven or when the statement being proven is secret shared among multiple verifiers. In these settings, minimizing the proof length is an important efficiency goal. While some constructions of fully linear PCPs are implicit in the literature, we also present new constructions that have sublinear proof size for "simple" or "structured" languages.
In the second part of the talk, we show how to apply fully linear PCPs to improve the efficiency of systems for multiparty computation, private messaging, private ad targeting, and more. For example, we use our new fully linear PCPs to convert semi-secure multiparty computation protocols into malicious-secure ones at sublinear additive communication cost, thereby improving the state of the art in multiparty computation.
Joint work with Dan Boneh, Elette Boyle, Henry Corrigan-Gibbs, and Yuval Ishai.
OptORAMa: Optimal Oblivious RAM
Gilad Asharov, Bar-Ilan University
Abstract:
Oblivious RAM (ORAM), first introduced in the ground-breaking work of Goldreich and Ostrovsky (STOC '87 and J. ACM '96) is a technique for provably obfuscating programs' access patterns, such that the access patterns leak no information about the programs' secret inputs. To compile a general program to an oblivious counterpart, it is well-known that \Omega(log N) amortized blowup is necessary, where N is the size of the logical memory. This was shown in Goldreich and Ostrovksy's original ORAM work for statistical security and in a somewhat restricted model (the so called \emph{balls-and-bins} model), and recently by Larsen and Nielsen (CRYPTO '18) for computational security.
A long standing open question is whether there exists an optimal ORAM construction that matches the aforementioned logarithmic lower bounds (without making large memory word assumptions, and assuming a constant number of CPU registers). In this paper, we resolve this problem and present the first secure ORAM with O(log N) amortized blowup, assuming one-way functions. Our result is inspired by and non-trivially improves on the recent beautiful work of Patel et al. (FOCS '18) who gave a construction with O(log N loglog N) amortized blowup, assuming one-way functions.
One of our building blocks of independent interest is a linear-time deterministic oblivious algorithm for tight compaction: Given an array of n elements where some elements are marked, we permute the elements in the array so that all marked elements end up in the front of the array. Our O(n) algorithm improves the previously best known deterministic or randomized algorithms whose running time is O(n log n) or O(n loglog n), respectively.
Joint work with Ilan Komargodski, Wei-Kai Lin, Kartik Nayak, Enoch Peserico, and Elaine Shi.
How to Trade Efficiency and Accuracy using Fault-Tolerant Computation
Hayim Shaul, IDC Herzliya
Abstract:
Recent years have witnessed improvements of several orders of magnitude in the implementations of homomorphic encryption (HE) schemes, leading to the development of numerous HE libraries and a growing number of use-cases. One of the influential improvements is due to the HEAAN scheme of Cheon et al. (Asiacrypt’17) that achieved a dramatic speedup in certain homomorphic arithmetic operations by allowing the encryption noise to overflow and corrupt some of the underlying plaintext’s bits. For certain machine learning motivated computations, this loss of accuracy does not impede the usefulness of the computation.
An interesting question is whether the speedup approach of HEAAN can be obtained without the loss of accuracy incurred. We address this question by viewing the error in HEAAN for single arithmetic operation as a noisy gate and employing an approach inspired by fault-tolerant computation of Boolean circuits going back to von Neumann (Automata Studies’56) to overcome the noise in each gate.
We show how to compile arithmetic circuits with noisy gates and noisy inputs in a way that keeps the variance of the accumulated error under control and its expectation at zero. When using HEAAN to homomorphically evaluate arithmetic circuits that were compiled with this compiler, we demonstrate a tradeoff between the efficiency of the compiled computation and its accuracy.
We show that for a class of computations, our compiled circuit will perform better than best known errorless HE schemes as well as the basic HEAAN approach. As a test case, we implement Welford’s algorithm for computing the variance of streaming data, and compare an homomorphic evaluation using HEAAN of the “standard” circuit for this task with the compiled circuit. Our results indicate that for the same precision level, using the compiler outperforms the standard approach both in terms of memory and running time. For example, for a stream of 45 values, the standard approach required 60 GigaBytes, whereas the compiled circuit required only 2 GigaBytes.
Joint work with Ran Cohen, Jonathan Frankle, Shafi Goldwasser, and Vinod Vaikuntanathan.
A Tight Parallel-Repetition Theorem for Random-Terminating Interactive Arguments
Iftach Haitner, Tel Aviv University
Abstract:
Soundness amplification is a central problem in the study of interactive protocols. While "natural" parallel repetition transformation is known to reduce the soundness error of some special cases of interactive arguments: three-message protocols and public-coin protocols, it fails to do so in the general case.
The only known round-preserving approach that applies to the general case of interactive arguments is Haitner's "random-terminating" transform [FOCS '09, SiCOMP '13]. Roughly speaking, a protocol 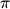 is first transformed into a new slightly modified protocol
is first transformed into a new slightly modified protocol 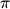
 , referred as the random terminating variant of
, referred as the random terminating variant of 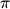 , and then parallel repetition is applied. Haitner's analysis shows that the parallel repetition of
, and then parallel repetition is applied. Haitner's analysis shows that the parallel repetition of 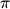
 does reduce the soundness error at a weak exponential rate. More precisely, if
does reduce the soundness error at a weak exponential rate. More precisely, if 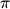 has m rounds and soundness error 1−
has m rounds and soundness error 1− , then
, then 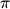 k
k , the k-parallel repetition of
, the k-parallel repetition of 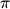
 , has soundness error (1-eps)^{eps k / m^4}. Since the security of many cryptographic protocols (e.g., binding) depends on the soundness of a related interactive argument, improving the above analysis is a key challenge in the study of cryptographic protocols.
, has soundness error (1-eps)^{eps k / m^4}. Since the security of many cryptographic protocols (e.g., binding) depends on the soundness of a related interactive argument, improving the above analysis is a key challenge in the study of cryptographic protocols.
In this work we introduce a different analysis for Haitner's method, proving that parallel repetition of random terminating protocols reduces the soundness error at a much stronger exponential rate: the soundness error of 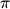 k
k is (1-eps)^{k/m}, only an m factor from the optimal rate of (1−
is (1-eps)^{k/m}, only an m factor from the optimal rate of (1− )k, achievable in public-coin and three-message protocols. We prove the tightness of our analysis by presenting a matching protocol.
)k, achievable in public-coin and three-message protocols. We prove the tightness of our analysis by presenting a matching protocol.
Joint work with Itay Berman and Eliad Tsfadia.
Local Proofs Approaching the Witness Length
Noga Ron-Zewi, Haifa University
Abstract:
Interactive oracle proofs (IOPs) are a hybrid between interactive proofs and PCPs. In an IOP the prover is allowed to interact with a verifier (like in an interactive proof) by sending relatively long messages to the verifier, who in turn is only allowed to query a few of the bits that were sent (like in a PCP).
In this work we construct, for a large class of NP relations, IOPs in which the communication complexity approaches the witness length. More precisely, for any NP relation for which membership can be decided in polynomial-time and bounded polynomial space (e.g., SAT, Hamiltonicity, Clique, Vertex-Cover, etc.) and for any constant \gamma > 0, we construct an IOP with communication complexity (1+\gamma) n, where n is the original witness length. The number of rounds as well as the number of queries made by the IOP verifier are constant.
This result improves over prior works on short IOPs/PCPs in two ways. First, the communication complexity in these short IOPs is proportional to the complexity of verifying the NP witness, which can be polynomially larger than the witness size. Second, even ignoring the difference between witness length and non-deterministic verification time, prior works incur (at the very least) a large constant multiplicative overhead to the communication complexity.
In particular, as a special case, we also obtain an IOP for Circuit-SAT with rate approaching 1: the communication complexity is (1+\gamma)t, for circuits of size t and any constant \gamma>0. This improves upon the prior state-of-the-art work of Ben Sasson et-al (ICALP, 2017) who construct an IOP for Circuit-SAT with rate that is a small (unspecified) constant bounded away from 0.
Our proof leverages recent constructions of high-rate locally testable tensor codes. In particular, we bypass the barrier imposed by the low rate of multiplication codes (e.g., Reed-Solomon, Reed-Muller or AG codes) - a core component in all known short PCP/IOP constructions.
Joint work with Ron Rothblum.
