Download Video: 720p
Lecture notes, page 1/11 •
[previous page] •
[next page] •
[PDF]
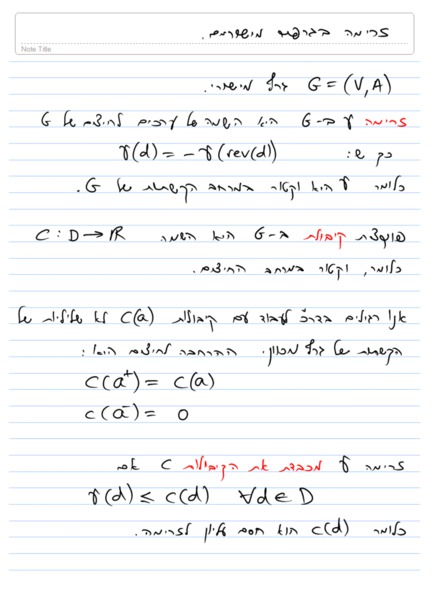
Lecture notes, page 1/11 • [previous page] • [next page] • [PDF]
[+] Circulations and maximum flow in st-planar graphs |
| We start our treatment of flow in planar graphs by relating circulations in the primal graph with face potentials in the planar dual. We show that the residual capacity of a dart with respect to a primal circulations is the slack cost of that dart in the dual with respect to the corresponding potential function. This establishes a connection between distances in the planar dual and capacity respecting circulations in the primal. We use this relation to give a linear-time algorithm for maximum st-flow when the source and sink lie on the same face. We conclide by briefly discussing a nearly linear-time algorithm for maximum st-flow in directed planar graphs. The algorithm resembles the MSSP algorithm. |
|
Download Video: 720p |
Lecture notes, page 1/11 •
[previous page] •
[next page] •
[PDF]
Lecture notes, page 1/11 • [previous page] • [next page] • [PDF] |
The video above should play if your web browser supports either modern Flash or HTML5 video with H.264 or WebM codec. The lecture notes should advance automatically. If you have any trouble with playback, email me.